Hi
@Quaoar,
Thank you for your careful and patient explanation. However, following the method you described, it appears that I can only obtain the outermost turn profile. Additionally, there seems to be an issue retrieving details inside the solid model, whether they deserve to be saved or not.
I have followed the method mentioned in the paper "Finding the maximum turnable state for mill/turn parts" to obtain the Maximum Turnable State (MTS):
1. Initially, I obtained the section curve from the solid model along the rotation axis at a certain step size using BRepAlgoAPI_Section in OCC. However, this process seemed too slow in some sections.
2. I then analyzed every loop in this section to determine its contribution to the final turn profile. This included identifying whether the loop is external (around material) or internal (not around material) and calculating the maximum and minimum distances of each loop to the rotation axis, as described in the mentioned paper. Through this method, I obtained some valid edges.
3. Subsequently, I constructed a rectangle face from each edge(the edge is perpendicular to the axis of rotation) and the step size.
4. My final objective is to aggregate all the faces to extract the curve of the boundary, which is what I need.
However, I encountered some problems during this process:
1. Initially, using BRepAlgoAPI_Section in OCC to obtain the curve seemed too slow in some sections.
2. Secondly, when discretizing the curve of the loop in each section into points, determining whether the closed curve is around the rotation axis, and calculating the maximum and minimum values of this loop, it appeared to lose some precision. Moreover, the calculation speed was too slow on some closed curves.
3. Lastly, if I were to create the final surface by aggregating many rectangular faces (the aggregation process has not been implemented yet) (I attempted to aggregate these TopoDS_Face using TopoDS_Compound and BRepBuilderAPI_Sewing, but the resulting TopoDS_Shape is not a TopoDS_Face. Moreover, in the synthesized TopoDS_Shape, the edges of the rectangles are retained, whereas I actually only need the outermost contour) , there was a noticeable jaggedness on some of the hypotenuses and curved edges.
I appreciate any insights or suggestions you may have regarding these challenges :)
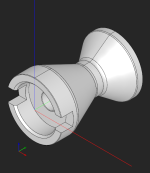
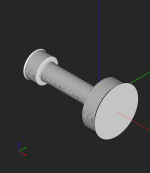
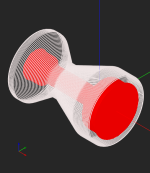
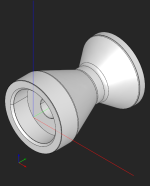
I have currently obtained results as shown in the following figure: