Slicing: looking for a non-convex hull algorithm

[Quaoar]

Hey guys. I'm now working on the slicing problem (not for 3D printing) where I need to intersect a CAD model with a stack of planes. The process is quite simple and can be outlined as follows:

1. Switch from B-rep to meshes.
2. Intersect mesh edges with planes (1-dimensional intersection, fast to compute).
3. Sort and connect all intersection points.



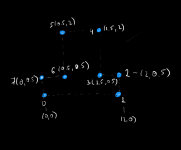
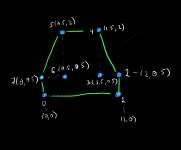
I am at the 3-rd stage right now. And for that I'm using the approach from this paper: [Moreira, A., & Santos, M. Y. (2007). Concave hull : a k-nearest neighbours approach for the computation of the region occupied by a set of points. Proceedings of the Second International Conference on Computer Graphics Theory and Applications, 61–68.] This is a pretty basic and sort of "blind" approach as whenever the algorithm gets into trouble, it attempts to increase the number of considered neighbors and repeats the whole process without any promise of success. I have its naive implementation which is not very efficient (as it uses dynamic memory allocation and some heavy OpenCascade calls that are better to be avoided) and not quite accurate. So I'm thinking either to improve what I have OR to find something better.

The problem looks quite standard, and it should have had been resolved thousands of times. Does anyone have any practical experience with this sort of slicing? What I need to have at the end is a closed planar polygon.

I'll post here on my progress if anyone's interested.

 

[Quaoar]

My implementation of Moreira's algorithm is sensitive to sparse configurations of point sets, e.g. for the following data set



the algorithm returns nothing better than the convex hull:



This happens because the next point is chosen according to the min-turn-angle rule and the turn from 2 to 4 yields a smaller angle than the turn from 2 to 3. It is possible to force K = 1, but then the successor point for 3 will be 6 as 6 is closer. My feeling is that trying to calibrate this whole thing (by accurate selection of K, introducing some distance/angle thresholds) is a waste of time as there always be a case that does not work. Maybe I have to feed Moreira with what it's designed for, i.e., with a dense point cloud, but it drives me back to the goddamn mesh refinement.

Am I overcomplicating things?

 

[A-U]

This looks promising: https://github.com/mapbox/concaveman (or rather the C++ port https://github.com/sadaszewski/concaveman-cpp ). An older library would be libqhull (look for alpha shapes). Looked into this topic briefly, but never tried it in the end.

 

[DanB]

On a previous slicer I've worked on, we used a bit more crude method. From the top of my head it went something like this:
1. Define all layers based on slicing parameters.
2. Find all facets in a particular layer(z-plane).
3. Do some trigonometry to find the intersection for each facet edge and the z-plane. Most facets will have two points of intersection, which defines a line that is stored to an array of all lines in the layer. Here we did a trick and stored each point with some precision(e.g 0.3f), such that we could easily find duplicate points that share an edge(neighbouring facets). In the edge-case when the intersection was in the corner of a facet, it's only stored as a point.
4. Then we just had to find which lines had duplicate "keys", connect the duplicate keys which produce a path. Lastly, the first point should in theory have the same "key" as the last key, and produce a closed polygon.

Sometimes we would run into issues when two points sharing an edge would not have the same "key", and the algorithm would produce "dead paths". I guess this happens because of some floating-point error. We fixed this by temporary scaling up the model. With some tricks along the way, it was quite fast actually.

 

[A-U]

Probably this is similar to the suggestion of DanB: you know in principle which trinagles are connected and you can map back the intersecting points to triangles so it should be possible to reconstruct the connectivity this way.

 

[Quaoar]

@A-U @DanB You're right, that should be a solution. I'll devote some more time to this subject in the coming days (had to switch to other things).

 

[DanB]

@A-U @DanB You're right, that should be a solution. I'll devote some more time to this subject in the coming days (had to switch to other things).

Another edge-case to be aware of is when an edge is parallel and on the plane.

 

[Quaoar]

Okay, I've done it as you guys proposed.







Using K-hull for that purpose was a stupid idea, so thank you for pointing this out.

Slicing a profile shape with holes:



The input triangulation does not have to be watertight, so we can compose it just by putting together all Poly_Triangulation data structures grabbed from the corresponding CAD faces:



100 slices in ~0.3 sec:



The source code of the solution is here: https://gitlab.com/ssv/lessons/-/blob/master/Lesson17_slice/main.cpp

 

[DanB]

Awesome! You even used the dictionary method

 

[bioan]

Excellent!!!
Looks very promising!!