Refine Poly_Triangulation meshes

[Quaoar]

Here in this topic, I'd like to accumulate some information on triangulation refinement in OpenCascade. As we all know, the meshes are stored in Poly_Triangulation data structures that are distributed by TopoDS_Face entities in the model. The standard open source mesher (BRepMesh) generates a CAD-like tessellation that is very sparse. It's an as-designed feature as the quality of such a mesh is "visualization-only." At the same time, I'd like to have a denser mesh that would allow running some advanced algorithms, such as thickness analysis or face accessibility checks. OCC offers a paid component to generate finer meshes, but we are not in the money-spending business here, right?

By the moment I start this thread, I have only the idea to refine the original sparse meshes so that we can generate denser triangulations by a set of simple techniques, such as midpoint refinement, edge collapse, edge flip, etc. I do not have any prototype so far, so let the journey begin.

First off, I came accross that paper: [Guo, J., Ding, F., Jia, X., & Yan, D. M. (2019). Automatic and high-quality surface mesh generation for CAD models. CAD Computer Aided Design, 109(April 2019), 49–59].

 

[Quaoar]

A couple of discoveries:

1. It really depends if you want your mesh to be conformal or not. The non-conformal meshes are not "watertight," but are easier to refine into.
2. It might not be necessary to refine the initial triangulation. Sometimes, it is enough to refine the derived triangulation obtained by merging the Poly_Triangulation patches using nodal gluing (check out the MeshMerge tool). However, in such a scenario your mesh data structure should preserve back-references to the originating CAD faces. I have this simplistic data structure for that purpose.
3. A question of a good mesh data structure that would allow for local refinement is really a key one. Here I wouldn't vote for any external package as, to remain on the cutting edge, you might need to invent something new depending on your app. I'm also close to thinking that you'd better store all mesh edges right away, with the back pointers to mesh elements. It's harder to maintain than just plain vectors of vertices plus triangles, but it really pays off once you're there. I did not follow that path though.

Down the road, I tried a couple of things to tweak BRepMesh to generate somewhat more dense triangulations. What I did was:

• Inserting internal vertices to faces like that (OpenCascade claims to keep internal vertices respected during the meshing process, and, indeed, I see them added to the BRepMesh internal structures; however, this leads to nothing in terms of constraint triangulation; I only saw that the presence of an extra vertex might introduce some degenerated triangles):
  

  const double u = 0.75*(uMin + uMax);
  const double v = 0.35*(vMin + vMax);
  BRepAdaptor_Surface bas(face);
  gp_Pnt P = bas.Value(u, v);
  TopoDS_Vertex V = BRepBuilderAPI_MakeVertex(P);
  V.Orientation(TopAbs_EXTERNAL);
  BRep_Builder().UpdateVertex( V, u, v, face, Precision::Confusion() );
  BRep_Builder().Add(face, V);

• Playing with all parameters of the mesher. Yeah, there's this "minSize" thingy that does not work or works in somewhat obscure ways that it's impossible to rely upon.
• Converting input geometries to splines. Converting your model to splines is the last thing you wanna do, and, thank goodness, it did not work either

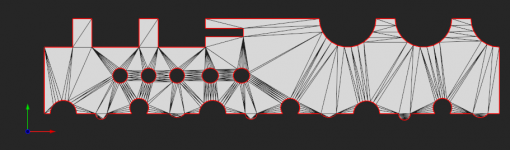
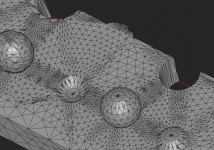
The conclusion is that you'd never get any better than this:



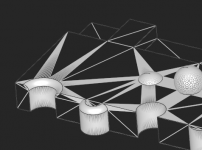
All my attempts to refine it with midpoint/midedge splits and edge flipping sort of slightly improved the situation, but not radically, and I am not happy with the results so far. The main problem is all these skinny triangles that are hard to get rid of. Now I'm thinking to try out octree-based layouts for planar faces. Even without merging them nicely across the boundaries with the rest of the model, you might get a good enough grid for some specific applications, like what I'm looking for (face accessibility analysis and thickness analysis).

Another option would be to try global remeshing, like something reported in [Botsch, M., & Kobbelt, L. (2004). A remeshing approach to multiresolution modeling. ACM International Conference Proceeding Series, 71, 185–192. https://doi.org/10.1145/1057432.1057457]. They use local mesh editing procedures, namely a few cycles (~5) like this:

1. Midpoint split all the edges that are longer than 4/3*l (where l is the target edge length).
2. Collapse all edges shorter than 4/5*l into their midpoints.
3. Flip edges in order to minimize the deviation from valence 6 (or 4 on boundaries).
4. Relocate vertices on the surface by tangential smoothing.

Why I think this paper is promising is that it claims to get rid of the degenerated or sliver triangles that kinda sucked me out. For the ray-based algorithms, I'd like to have higher-regularity meshes, and it is appealing to convert the initial triangulation into such. Simply because if you modify your input, you can simplify further processing. Not to mention that the algorithms like that can be reused down the road in a multitude of other algorithms I make living from. On the other hand, edge collapse (the gun to kill slivers) will inevitably distort the original boundary of a CAD face (well, its discretized version), and that does not sound good. Should I restrict it from touching the boundaries?

Btw, here is a nice presentation of various remeshing approaches. I skimmed it over searching for references, and it was quite instructive.



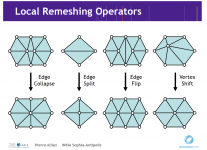
To confess, mesh refinement looks quite desperate as of now when I spent a week or so working on the basic refinement techniques (triangle subdivision, edge flipping, midedge subdivision) intensively. But I still miss quite a bunch of important ingredients (see the picture above for a gentleman's set of refining operators) and a good strategy for refinement. What I also discovered is that there's not much you can reuse from the Internet. For example, the famous J. R. Shewchuk's Triangle requires a license for commercial use, and that is something I could not afford for a couple of reasons.

 

[Quaoar]

Here is one link not to miss: http://meshrepair.org/

 

[Quaoar]

Here's a somewhat really crappy result that I managed to get after several trials. Few immediate notes follow:

1. The boundary is not preserved as I was too lazy to restrict edge flipping from touching it.
2. The performance is just super-awful.
3. It works for a single face only, but it should not be a big deal to extend it to multiple faces as we preserve face IDs in the mesh elements.
4. It's not automatic, so a strategy has to be elaborated.

Notice that edge collapse and edge flips are required to hunt down sliver triangles. I also used midpoint and midedge refinements, and finally smoothed this whole thing with Laplace with an overkill of 10000 iterations. The initial piece was this one:



What does it prove? Well, it proves that mesh refinement following a simple (non-Delaunay) stupid approach is kinda working. This result is something I wanted to achieve because if you do not manage to get your dream mesh manually, what are the chances you'll program a batch procedure to achieve that same goal.

Speaking about the whole strategy, here's how I see it.

1. Since BRepMesh does not want to respect min sizes mostly on planar faces, the refinement technique outlined above will be only concerned with the planar regions. All curved regions will be left to BRepMesh (unless I figure out how to kill that beast later on).
2. The input mesh is converted face-wise, i.e., all triangles remember the face IDs they belong to. Therefore, mesh boundaries are not topological, but rather semantic (a boundary is a link where face ID is switched).
3. For each planar face, we do the refinement having all the crap outlined above fixed.
4. The resulting model should be somewhat hybrid: planes are refined, curved regions are not.

 

[Quaoar]

Here's a bit better result after restricting edge collapse from touching the boundaries:



Some comments follow:

1. I seem to miss some validity checks for edge collapse as sometimes it ends up with non-manifold or free links. This is to be separated and tested on a smaller mesh region.
2. Performance is to be profiled. I did not care about it much, and just recomputed all the links after every single edge got collapsed. No surprises, it works slowly as hell.
3. The triangles on the boundaries can be refined as we do not really need to keep the boundary untouched. What we do need is to keep the final mesh watertight, i.e., if a boundary edge gets some modification, it should well propagate to another patch's triangle. If we allow that (with possibly some more control on how the shape is deformed), then we'll get rid of large or skinny triangles concentrated near the boundary.
4. What makes the mesh beautiful is smoothing. In the ultimate strategy, smoothing should be combined with refinement. E.g., one midpoint refinement can always be followed by smoothing.
5. Edge flips can make meshes worse in the terms of aspect ratio. That's stupid, and we'd better control the quality of triangles before and after edge flipping.
6. Given that almost all ingredients are there, it's probably time to put them together in some sort of a strategy. I'm thinking of a Tcl script.

 

[Quaoar]

Here's one more result I'm less ashamed of:





And the script (still manual) follows:

> poly-refine-midpoints -minarea 100
> poly-refine-midedges -minarea 100 -minlen 1
> poly-refine-midedges -minarea 10 -minlen 1
> poly-refine-midpoints -minarea 35
> poly-flip-edges
> poly-flip-edges
> poly-flip-edges
> poly-flip-edges
> poly-smooth -iter 1000
> poly-refine-midedges -minarea 10 -minlen 1
> poly-flip-edges
> poly-flip-edges
> poly-flip-edges
> poly-flip-edges
> poly-smooth -iter 1000
> poly-collapse-edges -maxlen 10
> poly-smooth -iter 1000
> poly-collapse-edges -maxlen 5
> poly-smooth -iter 1000
> poly-refine-midedges -minarea 10 -minlen 1
> poly-flip-edges
> poly-flip-edges
> poly-flip-edges
> poly-flip-edges
> poly-smooth -iter 1000
> poly-collapse-edges -maxlen 2
> poly-smooth -iter 1000
> poly-collapse-edges -maxlen 2
> poly-smooth -iter 1000

The problems summarized in the previous post still largely remain. Here's to recap:

1. I added some validity checks for edge collapse. Now the operation verifies that no degenerated triangles are going to emerge. However, if the mesh is not smoothed before running edge collapse, weird things still happen (we might miss edge-triangle intersection check here, see below). So, this thing is still to be separated and tested on a smaller mesh region.
2. Performance is to be profiled. I did eliminate the largest hotspot consisted of the recomputation of the cached links on each collapse, but it's still slow. Not as hell though.
3. The triangles on the boundaries can be refined as we do not really need to keep the boundary untouched. What we do need is to keep the final mesh watertight, i.e., if a boundary edge gets some modification, it should well propagate to another patch's triangle. If we allow that (with possibly some more control on how the shape is deformed), then we'll get rid of large or skinny triangles concentrated near the boundary.
4. What makes the mesh beautiful is smoothing. In the ultimate strategy, smoothing should be combined with refinement. E.g., one midpoint refinement can always be followed by smoothing. Also, I want to get rid of the VTK algorithm here and support mesh smoothing natively to avoid conversion overheads.
5. Edge flips can make meshes worse in the terms of aspect ratio. That's stupid, and we'd better control the quality of triangles before and after edge flipping. For that, I'll have to add a simple aspect ratio (or, better, scaled Jacobian) check, so that the triangles tending to become worse than the specified threshold value will not be touched. Still, as with the edge collapse operator, it's good to have a flag like "-force" to enable edge flips if you know what exactly you're doing (or if you want to debug the thing).
6. Given that almost all ingredients are there, it's probably time to put them together in some sort of a strategy. I'm thinking of a Tcl script.
7. I now sort all triangles by area beforehand, so that the larger triangles get priority in refinement. However, somewhere near the boundaries, the splitting is still not perfect. I'll probably have to check this thing closer after I make it work for the entire CAD model mesh (not a single face as of now).
8. Hell, tests. I'll probably need to print out all the API functions I've got in the mesh data structure and carefully test each one. That's a boring time-eating thing, but it's a must.
9. Remove redundant vertices of the valence 3 (does not require retriangulation of the newly emerged polygons).

 

[Quaoar]

Here's a couple of updates:

1. Edge flips now control the scaled Jacobian metric of the triangles. If the min Jacobian after the flip is worse (i.e., its value is less) than it was initially, such flip isn't going to happen. The implication of such an enhancement is quite sweet: we can now limit the number of flip attempts and stop worrying that flipping would only mess up an acceptable-quality mesh. Now it kinda converges, and each new iteration makes the mesh better or at least not worse than before.
2. It will be nice to add another function which is named "Edge Split" in the presentation by Inria (see above). It should help improving tiny triangles that could not be fixed by edge flips (you will easily identify such on the image below):

 

[Quaoar]

One more link not to miss (comes up with the removal of redundant mesh points operator that, I guess, might be useful according to what I see on the intermediate meshes during this long but exciting investigation): https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0184206

It also contains some considerations on the less greedy Laplacian smoothing (smooth only the badly shaped triangles) and reports an algorithm for triangle-edge intersection that we could try to integrate with the edge collapse operator as it sometimes gives bad results.

 

[Quaoar]

Was messing around with refinement operators and edge collapse in particular. This edge collapse operator has two inherent problems as of now, and one external problem looking from the caller code's perspective:

• It does not respect boundaries, although we have all necessary information to fix that (as we have face IDs associated with all triangles).
• Performance is awful (animation does not show this).
• It's better to sort all the edges by their length and collapse starting from the min-length edges.

 

[Quaoar]

Okay, planar refinement is more or less done and integrated to Analysis Situs with some compromises. I'll continue working on that subject and will come back here if anything interesting shows up. A more detailed overview will be available in the docs and (maybe) in the corresponding youtube video.