A full quadrilateral mesh generation method based on the Q-Morph algorithm

[calciffer]

This is not a question post, and this is the first one of a series of posts.
I just want to share how to generate a fully quad mesh based on the Q-Morph algorithm. The main theory is based on the following two papers:

1. Owen, S. J., Staten, M. L., Canann, S. A., & Saigal, S. (1999). Q-Morph: An indirect approach to advancing front quad meshing. International Journal for Numerical Methods in Engineering, 44(9), 1317-1340.
2. 汪攀,张见明,韩磊等.基于带约束前沿推进的四边形网格生成方法.湖南大学学报(自然科学版),2017,44(08):29-34.

The third-party libraries I used include netgen, vtk, openmesh, and opencascade. I used the opencascade library to read geometry files, the netgen library to perform triangulation, the polymesh data structure from the openmesh library to store node and element information, and the vtk library to display the mesh.

I ran some tests on the code in release mode, and here are some examples:





As you can see from the pictures, this code is just a prototype and far from perfect, and there are still the following problems:

1. How to control the number of boundary nodes generated by netgen to be even, if the number of total boundary nodes is odd, there will always be a triangle left in the final quad mesh result;
2. The final generated mesh still needs further processing, such as close the node and local adjust. Like the pictures shown below;
3. Unable to control grid flow;
4. The robustness of the procedure still needs to be improved.

Like the pictures shown below:

 

[calciffer]

This is the second one of a series of posts, here we introduce some basic, functional functions.
You can easily tell what these functions do from their names

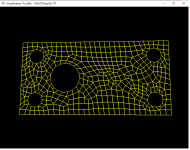
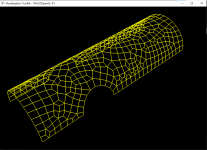
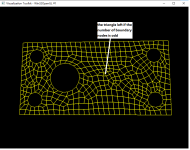
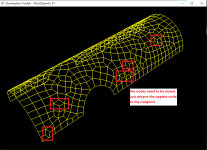
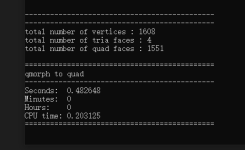
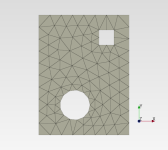
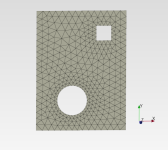
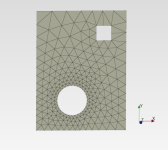
void netGenTriangulation(const TopoDS_Shape& thShape,
                         PolyMesh&           theMesh)
{
    Bnd_Box aabb;
    BRepBndLib::Add(thShape, aabb, false);
    const double diag = std::sqrt(aabb.SquareExtent());

    std::cout << "diag of shape: " << diag << std::endl;

    netgen::MeshingParameters& mp = netgen::mparam;
    mp.minh = 0.0;
    mp.maxh = 0.05 * diag;
    mp.uselocalh = true;
    mp.secondorder = false;
    mp.grading = 0.3;

    nglib::Ng_Init();

    netgen::OCCGeometry occgeo;
    occgeo.shape = thShape;
    occgeo.changed = 1;
    occgeo.BuildFMap();
    occgeo.CalcBoundingBox();

    // Resulting mesh.
    netgen::Mesh ngMesh;

    // Mesh building
    netgen::OCCSetLocalMeshSize(occgeo, ngMesh);
    netgen::OCCFindEdges(occgeo, ngMesh);
    netgen::OCCMeshSurface(occgeo, ngMesh, netgen::MESHCONST_OPTSURFACE);

    const int nbNodes = (int)ngMesh.GetNP();
    const int nbTriangles = (int)ngMesh.GetNSE();

    for (int i = 1; i <= nbNodes; ++i)
    {
        const netgen::MeshPoint& point = ngMesh.Point(netgen::PointIndex(i));
        PolyMesh::VertexHandle vh = theMesh.add_vertex(PolyMesh::Point(point[0], point[1], point[2]));
    }
    

    for (int i = 1; i <= nbTriangles; ++i)
    {
        const netgen::Element2d& elem = ngMesh.SurfaceElement(netgen::ElementIndex(i));
        if (elem.GetNP() == 3)
        {
            PolyMesh::FaceHandle fh = theMesh.add_face(
                PolyMesh::VertexHandle(elem[0] - 1),
                PolyMesh::VertexHandle(elem[1] - 1),
                PolyMesh::VertexHandle(elem[2] - 1));
        }

        if (elem.GetNP() == 4)
        {
            PolyMesh::FaceHandle fh = theMesh.add_face(
                PolyMesh::VertexHandle(elem[0] - 1),
                PolyMesh::VertexHandle(elem[1] - 1),
                PolyMesh::VertexHandle(elem[2] - 1),
                PolyMesh::VertexHandle(elem[3] - 1));
        }
    }

    ngMesh.DeleteMesh();
    nglib::Ng_Exit();

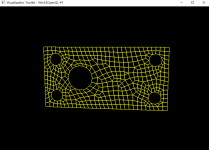
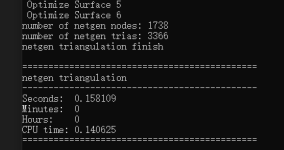
    std::cout << "number of netgen nodes: " << nbNodes << std::endl;
    std::cout << "number of netgen trias: " << nbTriangles << std::endl;
    std::cout << "netgen triangulation finish" << std::endl;
}





double getDistance(const PolyMesh& theMesh,
    const PolyMesh::VertexHandle& vh1,
    const PolyMesh::VertexHandle& vh2)
{
    OpenMesh::Vec3f p1 = theMesh.point(vh1);
    OpenMesh::Vec3f p2 = theMesh.point(vh2);
    double distace = (p2 - p1).norm();
    return distace;
}





double getAngle(const PolyMesh& theMesh,
    const PolyMesh::VertexHandle& v1,
    const PolyMesh::VertexHandle& v2,
    const PolyMesh::VertexHandle& v3)
{
    PolyMesh::Normal v2v1 = theMesh.point(v1) - theMesh.point(v2);
    PolyMesh::Normal v2v3 = theMesh.point(v3) - theMesh.point(v2);

    v2v1.normalize();
    v2v3.normalize();

    double dot = v2v1 | v2v3;
    
    // consider the calculation precision
    if (dot > 1.0)
        return 0.0;
    if (dot < -1.0)
        return 180.0;
    double angle = std::acos(dot);
    
    return angle * 180.0 / M_PI;
}


double getArea(const PolyMesh& theMesh,
    const PolyMesh::VertexHandle& v1,
    const PolyMesh::VertexHandle& v2,
    const PolyMesh::VertexHandle& v3)
{
    double d1 = getDistance(theMesh, v1, v2);
    double d2 = getDistance(theMesh, v2, v3);
    double d3 = getDistance(theMesh, v1, v3);
    double d = (d1 + d2 + d3) / 2.0;

    double area = sqrt(d*(d - d1)*(d - d2)*(d - d3));

    return area;
}



double getTriaArea(const PolyMesh& theMesh,
    const PolyMesh::FaceHandle& fh)
{
    PolyMesh::HalfedgeHandle heh = theMesh.halfedge_handle(fh);
    PolyMesh::VertexHandle vh1 = theMesh.to_vertex_handle(heh);
    PolyMesh::VertexHandle vh2 = theMesh.to_vertex_handle(theMesh.next_halfedge_handle(heh));
    PolyMesh::VertexHandle vh3 =
        theMesh.to_vertex_handle(theMesh.next_halfedge_handle(theMesh.next_halfedge_handle(heh)));

    return getArea(theMesh, vh1, vh2, vh3);
}



double getTriaQualityFactor(const PolyMesh& theMesh,
    const PolyMesh::FaceHandle& fh)
{
    PolyMesh::HalfedgeHandle heh = theMesh.halfedge_handle(fh);
    PolyMesh::VertexHandle vh1 = theMesh.to_vertex_handle(heh);
    PolyMesh::VertexHandle vh2 = theMesh.to_vertex_handle(theMesh.next_halfedge_handle(heh));
    PolyMesh::VertexHandle vh3 =
        theMesh.to_vertex_handle(theMesh.next_halfedge_handle(theMesh.next_halfedge_handle(heh)));

    return getTriaQualityFactor(theMesh, vh1, vh2, vh3);
}




double getTriaQualityFactor(const PolyMesh& theMesh,
    const PolyMesh::VertexHandle& v1,
    const PolyMesh::VertexHandle& v2,
    const PolyMesh::VertexHandle& v3)
{

    double d1 = getDistance(theMesh, v1, v2);
    double d2 = getDistance(theMesh, v2, v3);
    double d3 = getDistance(theMesh, v1, v3);
    double d = (d1 + d2 + d3) / 2.0;

    double area = sqrt(d*(d - d1)*(d - d2)*(d - d3));
    
    return area * 4.0 * 1.7320508 / (d1*d1+d2*d2+d3*d3);
}





double getQuadQualityFactor(const PolyMesh& theMesh,
    const PolyMesh::VertexHandle& v1,
    const PolyMesh::VertexHandle& v2,
    const PolyMesh::VertexHandle& v3,
    const PolyMesh::VertexHandle& v4)
{

    double triaQuality1 = getTriaQualityFactor(theMesh, v1, v2, v3);
    double triaQuality2 = getTriaQualityFactor(theMesh, v1, v2, v4);
    double triaQuality3 = getTriaQualityFactor(theMesh, v3, v4, v2);
    double triaQuality4 = getTriaQualityFactor(theMesh, v3, v4, v1);

    std::vector<double> triaQualities = { triaQuality1 ,triaQuality2, triaQuality3, triaQuality4};
    std::sort(triaQualities.begin(), triaQualities.end(), std::greater<double>());

    return triaQualities[2] * triaQualities[3] / triaQualities[0] / triaQualities[1];
}




double getFaceAngle(const PolyMesh& theMesh,
    const PolyMesh::VertexHandle& v1,
    const PolyMesh::VertexHandle& v2,
    const PolyMesh::VertexHandle& v3,
    const PolyMesh::VertexHandle& v4)
{
    // Calculate the Angle between the triangular faces formed by v1, v2, v3
        // and the triangular faces formed by v2, v1, v4
    // If v3, v4 are in the same plane as v1, v2,
        // return 0 if v3, v4 are on the same side of v1, v2 and return 180 on different sides
    PolyMesh::Point p1 = theMesh.point(v1);
    PolyMesh::Point p2 = theMesh.point(v2);
    PolyMesh::Point p3 = theMesh.point(v3);
    PolyMesh::Point p4 = theMesh.point(v4);


    PolyMesh::Normal n1 = (p1 - p3) % (p2 - p3);
    n1.normalize();

    PolyMesh::Normal n2 = (p2 - p4) % (p1 - p4);
    n2.normalize();

    double dot = n1 | n2;
    if (dot > 1.0)
        return 180.0;
    if (dot < -1.0)
        return 0.0;
    double angle = std::acos(dot);
    double rs = 180.0 - angle * 180.0 / M_PI;
    return rs;
}




bool checkVetexConnection(PolyMesh& theMesh,
    const PolyMesh::VertexHandle& vh1,
    const PolyMesh::VertexHandle& vh2)
{
    // Iterate over the neighboring vertex of vertex 1
    for (PolyMesh::VertexVertexIter vv_it = theMesh.vv_begin(vh1); vv_it != theMesh.vv_end(vh1); ++vv_it)
    {
        PolyMesh::VertexHandle vh = *vv_it;
        if (vh == vh2)
        {
            return true;
        }
    }
    return false;
}













bool checkIsolatedTriangle(PolyMesh& theMesh)
{
    // Count the number of triangular faces
    int numTriangles = 0;
    for (PolyMesh::FaceIter f_it = theMesh.faces_begin(); f_it != theMesh.faces_end(); ++f_it)
    {
        PolyMesh::FaceHandle fh = *f_it;
        if (theMesh.valence(fh) == 3)
        {
            numTriangles++;
        }
    }

    // if the number of triangular faces is zero, return false
    if (numTriangles == 0)
    {
        return false;
    }

    // Count the number of edges adjacent to only one triangular face
        // and compare to the number of triangular faces
    int numEdgesWithOneTriangle = 0;

    // Iterate over all edges
    for (PolyMesh::EdgeIter e_it = theMesh.edges_begin(); e_it != theMesh.edges_end(); ++e_it)
    {
        PolyMesh::EdgeHandle eh = *e_it;

        // obtain the two face_handles of the edge
        PolyMesh::HalfedgeHandle heh1 = theMesh.halfedge_handle(eh, 0);
        PolyMesh::HalfedgeHandle heh2 = theMesh.halfedge_handle(eh, 1);
        PolyMesh::FaceHandle fh1 = theMesh.face_handle(heh1);
        PolyMesh::FaceHandle fh2 = theMesh.face_handle(heh2);

        // if the first is tria face and another is quad face or invalid
        if (fh1.is_valid() && theMesh.valence(fh1) == 3 &&
            (!fh2.is_valid() || (fh2.is_valid() && theMesh.valence(fh2) == 4)))
        {
            numEdgesWithOneTriangle++;
        }
        else if (fh2.is_valid() && theMesh.valence(fh2) == 3 &&
            (!fh1.is_valid() || (fh1.is_valid() && theMesh.valence(fh1) == 4)))
        {
            numEdgesWithOneTriangle++;
        }
    }

    if (numEdgesWithOneTriangle != numTriangles * 3)
    {
        return true;
    }
    else
    {
        return false;
    }
}

 

[synt]

interesting, probably each edge division need to be set for better results as it shown in paper references.


result,

 

[calciffer]

Here is the third post of a series of posts, we need to figure out how to keep single connected domain, or in other words, under what situation can we create a quadrilateral?

The picture below is taken from the paper

汪攀,张见明,韩磊等.基于带约束前沿推进的四边形网格生成方法.湖南大学学报(自然科学版),2017,44(08):29-34.

The bold lines in the picture means the edges between a quadrilateral and a triangular or the boundary edges of triangulation. Shaded regions represent quadrilateral regions or regions outside the triangulation boundary. Before we use A, B, C and D to create a quad, we need to keep simply connected domain by counting the number of "front edge" of the to-be-created quad and the number of nodes belong to "front edge".
It can be seen from the picture that in the cases shown in a, d, f, i and j, the triangular region is still a single connected domain after the quadrilateral is generated by ABCD four points.

Wang Pan et al. proposed the following rule to judge whether a simply connected region can still be maintained after generating a quadrilateral:

1. nFrontNode=2;
2. nFrontNode=3 && nFrontEdge=2;
3. nFrontNode=4 && nFrontEdge>2;

And the code is as follow

int checkQuadFeasibility(PolyMesh& theMesh,
    const PolyMesh::VertexHandle& vh1,
    const PolyMesh::VertexHandle& vh2,
    const PolyMesh::VertexHandle& vh3,
    const PolyMesh::VertexHandle& vh4)
{

    int edgeNum = 0;
    int nodeNum = 0;

    std::vector<std::vector<PolyMesh::VertexHandle>> quadEdges =
        { {vh1, vh2}, {vh2, vh3} , {vh3, vh4} ,{vh4, vh1} };

    for (auto edgeVertices : quadEdges) {
        for (PolyMesh::VertexEdgeIter ve_it = theMesh.ve_iter(edgeVertices[0]); ve_it.is_valid(); ++ve_it) {
            PolyMesh::HalfedgeHandle heh1 = theMesh.halfedge_handle(*ve_it, 0);
            PolyMesh::HalfedgeHandle heh2 = theMesh.halfedge_handle(*ve_it, 1);
            PolyMesh::VertexHandle vh1 = theMesh.to_vertex_handle(heh1);
            PolyMesh::VertexHandle vh2 = theMesh.to_vertex_handle(heh2);

            if (vh1 == edgeVertices[1] || vh2 == edgeVertices[1]) {
                PolyMesh::FaceHandle fh1 = theMesh.face_handle(heh1);
                PolyMesh::FaceHandle fh2 = theMesh.face_handle(heh2);
                if (fh1.is_valid() && theMesh.valence(fh1) == 3 &&
                        (!fh2.is_valid() || (fh2.is_valid() && theMesh.valence(fh2) == 4)))
                {
                    edgeNum++;
                }
                else if (fh2.is_valid() && theMesh.valence(fh2) == 3 &&
                        (!fh1.is_valid() || (fh1.is_valid() && theMesh.valence(fh1) == 4)))
                {
                    edgeNum++;
                }
                break;
            }
        }
    }

    std::vector<PolyMesh::VertexHandle > quadVertices = { vh1, vh2, vh3, vh4 };

    for (auto vh : quadVertices) {
        for (PolyMesh::VertexEdgeIter ve_it = theMesh.ve_iter(vh); ve_it.is_valid(); ++ve_it) {
            PolyMesh::EdgeHandle eh = *ve_it;
            PolyMesh::HalfedgeHandle heh1 = theMesh.halfedge_handle(eh, 0);
            PolyMesh::HalfedgeHandle heh2 = theMesh.halfedge_handle(eh, 1);
            PolyMesh::FaceHandle fh1 = theMesh.face_handle(heh1);
            PolyMesh::FaceHandle fh2 = theMesh.face_handle(heh2);
            if (fh1.is_valid() && theMesh.valence(fh1) == 3 &&
                (!fh2.is_valid() || (fh2.is_valid() && theMesh.valence(fh2) == 4)))
            {
                nodeNum++;
                break;
            }
            else if (fh2.is_valid() && theMesh.valence(fh2) == 3 &&
                (!fh1.is_valid() || (fh1.is_valid() && theMesh.valence(fh1) == 4)))
            {
                nodeNum++;
                break;
            }
        }
    }

    if (nodeNum == 2) {
        return 1;
    }
    else if (nodeNum == 3 && edgeNum == 2) {
        return 1;
    }
    else if (nodeNum == 4 && edgeNum > 2) {
        return 1;
    }
    else if (nodeNum == 4 && edgeNum == 2) {
        return -1;
    }
    else {
        return 0;
    }
}

In addition, the return value of 0 of the above function means that after creating the quadrilateral element the triangular region is no longer a single connected domain. The return value of 1 means ok. Please note that the return value of the function can also be -1, which is a special setting that I will explain in the next post

 

[Quaoar]

That all looks amazingly interesting, although it would require a deep dive into quadmesh generation field to constructively comment on your achievements. I'll pin the topic to be always on top for now, so other folks can find it more easily.

 

[calciffer]

This is the fourth in a series of posts where I want to give a brief introduction to the openmesh library since the whole program is based on the polymesh data structure from the openmesh library.



In the above picture, there are a total of 3 faces, the black bold line represents the edge of the face, the green arrow line represents the halfedge, and any edge contains two halfedges, even if this edge lies on the boundary. Every halfedge contains the face on which it lies, and if this face is invalid, this edge lies on the boundary. The purple arrow line represents the normal of the face, and you can easily get their direction based on the right-hand rule.

More importantly, you can calculate the angle between two adjacent faces based on the Angle between their normals. You can see that the angle between face1 and face2 is 180 and the angle between their normals is 0.

Here are some basic, functional functions that might help you understand polymesh data structures:

void findTriaEdges(PolyMesh& theMesh,
    std::vector<PolyMesh::EdgeHandle>& theEdges)
{
    for (PolyMesh::EdgeIter e_it = theMesh.edges_begin(); e_it != theMesh.edges_end(); ++e_it)
    {
        PolyMesh::EdgeHandle eh = *e_it;

        PolyMesh::HalfedgeHandle heh1 = theMesh.halfedge_handle(eh, 0);
        PolyMesh::HalfedgeHandle heh2 = theMesh.halfedge_handle(eh, 1);
        PolyMesh::FaceHandle fh1 = theMesh.face_handle(heh1);
        PolyMesh::FaceHandle fh2 = theMesh.face_handle(heh2);

        if (fh1.is_valid() && theMesh.valence(fh1) == 3 &&
            (!fh2.is_valid() || (fh2.is_valid() && theMesh.valence(fh2) == 4)))
        {
            theEdges.push_back(eh);
        }
        else if (fh2.is_valid() && theMesh.valence(fh2) == 3 &&
            (!fh1.is_valid() || (fh1.is_valid() && theMesh.valence(fh1) == 4)))
        {
            theEdges.push_back(eh);
        }
    }
}



void findFaceEdges(PolyMesh& theMesh,
    std::vector<PolyMesh::EdgeHandle>& theEdges)
{
    for (PolyMesh::EdgeIter e_it = theMesh.edges_begin(); e_it != theMesh.edges_end(); ++e_it)
    {
        PolyMesh::EdgeHandle eh = *e_it;

        PolyMesh::HalfedgeHandle heh1 = theMesh.halfedge_handle(eh, 0);
        PolyMesh::HalfedgeHandle heh2 = theMesh.halfedge_handle(eh, 1);
        PolyMesh::FaceHandle fh1 = theMesh.face_handle(heh1);
        PolyMesh::FaceHandle fh2 = theMesh.face_handle(heh2);

        if (fh1.is_valid() && !fh2.is_valid())
        {
            theEdges.push_back(eh);
        }
        else if (fh2.is_valid() && !fh1.is_valid())
        {
            theEdges.push_back(eh);
        }
    }
}










void getEdgeVertices(PolyMesh& theMesh,
    std::vector<PolyMesh::EdgeHandle>& theEdges,
    std::set<PolyMesh::VertexHandle>& theVertices)
{

    for (auto eh : theEdges) {
        PolyMesh::HalfedgeHandle heh1 = theMesh.halfedge_handle(eh, 0);
        PolyMesh::HalfedgeHandle heh2 = theMesh.halfedge_handle(eh, 1);
        PolyMesh::VertexHandle vh1 = theMesh.to_vertex_handle(heh1);
        PolyMesh::VertexHandle vh2 = theMesh.to_vertex_handle(heh2);
        theVertices.insert(vh1);
        theVertices.insert(vh2);
    }
}


void jacobiLaplaceSmooth(PolyMesh& theMesh)
{
    OpenMesh::Smoother::SmootherT< PolyMesh >::Component com =
        OpenMesh::Smoother::SmootherT< PolyMesh >::Tangential;
    OpenMesh::Smoother::SmootherT< PolyMesh >::Continuity con =
        OpenMesh::Smoother::SmootherT< PolyMesh >::C0;

    OpenMesh::Smoother::JacobiLaplaceSmootherT<PolyMesh> smoother(theMesh);
    smoother.initialize(com, con);
    smoother.smooth(5);


    /*try
    {
        if (!OpenMesh::IO::write_mesh(theMesh, "jacobiLaplace_after.vtk"))
        {
            std::cerr << "Cannot write mesh to file 'jacobiLaplace_after.vtk'" << std::endl;
            return;
        }
    }
    catch (std::exception& x)
    {
        std::cerr << x.what() << std::endl;
        return;
    }*/



    std::cout << "jacobiLaplaceSmooth " << "---- finish" << std::endl;
}



// v1-------v2
//  |       |
//  |       |
//  |       |
// v4-------v3
// for v1 in [list v1 v2 v3 v4]  return [list v1 v2 v4 v3]

std::vector<PolyMesh::VertexHandle> sortQuadVertices(const std::vector<PolyMesh::VertexHandle>& theVertices,
    const PolyMesh::VertexHandle& theVertex)
{
    // find the index of the node in the list
    int idx = std::find(theVertices.begin(), theVertices.end(), theVertex) - theVertices.begin();

    if (idx == 0) {
        return { theVertex, theVertices[1], theVertices[3], theVertices[2] };
    }
    else if (idx == 1) {
        return { theVertex, theVertices[0], theVertices[2], theVertices[3] };
    }
    else if (idx == 2) {
        return { theVertex, theVertices[1], theVertices[3], theVertices[0] };
    }
    else {
        return { theVertex, theVertices[0], theVertices[2], theVertices[1] };
    }
}


// Check whether vh1 and vh2 are opposite vertices of the quadrilateral faces
bool checkRecoveryFeasibility(PolyMesh& theMesh,
    const PolyMesh::VertexHandle& vh1,
    const PolyMesh::VertexHandle& vh2)
{
    std::vector<PolyMesh::FaceHandle> adjQuadFaces;
    for (PolyMesh::VertexFaceIter vf_it = theMesh.vf_iter(vh1); vf_it.is_valid(); ++vf_it) {
        if (theMesh.valence(*vf_it) == 4) {
            adjQuadFaces.push_back(*vf_it);
        }
    }

    if (adjQuadFaces.size() == 0) {
        return true;
    }
    else {
        for (auto qh : adjQuadFaces) {
            std::vector<PolyMesh::VertexHandle> faceVertices;
            for (PolyMesh::FaceVertexIter fv_it = theMesh.fv_iter(qh); fv_it.is_valid(); ++fv_it) {
                faceVertices.push_back(*fv_it);
            }
            if (sortQuadVertices(faceVertices, vh1)[3] == vh2) {
                return false;
            }
        }

    }
    return true;
}

 

[calciffer]

This is the fist part of the fifth post of a series of posts, focusing on the implementation of part of the algorithm presented in the following paper. I have changed some parameters. Reading the paper carefully will help you read the code below.

Owen, S. J., Staten, M. L., Canann, S. A., & Saigal, S. (1999). Q-Morph: An indirect approach to advancing front quad meshing. International Journal for Numerical Methods in Engineering, 44(9), 1317-1340.

bool checkTriaByVertex(PolyMesh& mesh, 
    const PolyMesh::VertexHandle& v1, 
    const PolyMesh::VertexHandle& v2, 
    const PolyMesh::VertexHandle& v3)
{
    for (PolyMesh::FaceIter f_it = mesh.faces_begin(); f_it != mesh.faces_end(); ++f_it) {
        int count = 0;
        for (PolyMesh::FaceVertexIter fv_it = mesh.fv_iter(*f_it); fv_it.is_valid(); ++fv_it) {
            if (*fv_it == v1 || *fv_it == v2 || *fv_it == v3) {
                count++;
            }
        }
        if (count == 3) {
            return true;
        }
    }
    return false;
}

PolyMesh::VertexHandle getThirdVertex(PolyMesh& theMesh,
    const PolyMesh::VertexHandle& vh1,
    const PolyMesh::VertexHandle& vh2,
    const std::vector<PolyMesh::EdgeHandle>& theEdges)
{
    PolyMesh::VertexHandle vh;

    std::set< PolyMesh::VertexHandle> vertices;
    
    for (auto theEdge: theEdges) {
        if (theMesh.is_valid_handle(theEdge)) {
            PolyMesh::HalfedgeHandle heh1 = theMesh.halfedge_handle(theEdge, 0);
            PolyMesh::HalfedgeHandle heh2 = theMesh.halfedge_handle(theEdge, 1);
            PolyMesh::VertexHandle theVh1 = theMesh.to_vertex_handle(heh1);
            PolyMesh::VertexHandle theVh2 = theMesh.to_vertex_handle(heh2);

            if (theVh1 == vh1) {
                if (theVh2 != vh2) {
                    return theVh2;
                }
            }
            else if (theVh2 == vh1) {
                if (theVh1 != vh2) {
                    return theVh1;
                }
            }
        }
        
    }
    return vh;
}



std::vector<std::pair<PolyMesh::VertexHandle, double>> getVertexAngleList(PolyMesh& theMesh,
    const PolyMesh::VertexHandle& currentVertex,
    const PolyMesh::VertexHandle& secondVertex,
    const PolyMesh::VertexHandle& thirdVertex)
{
    PolyMesh::Point tempVertexpoint;

    double total_angle = 0;
    std::vector<std::pair<PolyMesh::VertexHandle, double>> vertexAngleList;
    vertexAngleList.push_back(std::make_pair(secondVertex, total_angle));

    PolyMesh::VertexHandle tempVertex = secondVertex;
    std::vector<PolyMesh::FaceHandle> processedFaces;
    while (tempVertex != thirdVertex) {
        std::vector<PolyMesh::FaceHandle> adjFaces;
        
        for (PolyMesh::VertexFaceIter vf_it = theMesh.vf_iter(currentVertex); vf_it.is_valid(); ++vf_it) {
            if (tempVertex == secondVertex) {
                if (theMesh.valence(*vf_it) == 3) {
                    adjFaces.push_back(*vf_it);
                }
            }
            else {
                adjFaces.push_back(*vf_it);
            }
        }
        for (auto adjfh : adjFaces) {
            std::vector<PolyMesh::VertexHandle> faceVertices;
            for (PolyMesh::FaceVertexIter fv_it = theMesh.cfv_iter(adjfh); fv_it.is_valid(); ++fv_it) {
                faceVertices.push_back(*fv_it);
            }
            if (std::find(faceVertices.begin(), faceVertices.end(), currentVertex) != faceVertices.end() &&
                std::find(faceVertices.begin(), faceVertices.end(), tempVertex) != faceVertices.end() &&
                std::find(processedFaces.begin(), processedFaces.end(), adjfh) == processedFaces.end()) {

                std::vector<PolyMesh::VertexHandle> sortVertices;
                if (theMesh.valence(adjfh) == 4) {
                    std::vector<PolyMesh::VertexHandle> tempSortVertices = sortQuadVertices(faceVertices, currentVertex);
                    sortVertices.push_back(tempSortVertices[0]);
                    sortVertices.push_back(tempSortVertices[1]);
                    sortVertices.push_back(tempSortVertices[2]);
                }
                else {
                    sortVertices = faceVertices;
                }
                sortVertices.erase(std::remove(sortVertices.begin(), sortVertices.end(), currentVertex),
                    sortVertices.end());
                sortVertices.erase(std::remove(sortVertices.begin(), sortVertices.end(), tempVertex), sortVertices.end());
                PolyMesh::VertexHandle objectVertex = sortVertices[0];

                total_angle = total_angle + getAngle(theMesh, tempVertex, currentVertex, objectVertex);
                vertexAngleList.push_back(std::make_pair(objectVertex, total_angle));

                tempVertex = objectVertex;

                processedFaces.push_back(adjfh);

                break;
            }
        }
    }
    return vertexAngleList;
}

 

[calciffer]

This is the second part of the fifth post of a series of posts, focusing on the implementation of part of the algorithm presented in the following paper.

Owen, S. J., Staten, M. L., Canann, S. A., & Saigal, S. (1999). Q-Morph: An indirect approach to advancing front quad meshing. International Journal for Numerical Methods in Engineering, 44(9), 1317-1340.

PolyMesh::VertexHandle getAlignVertex(PolyMesh& theMesh,
    const PolyMesh::VertexHandle& currentVH,
    const PolyMesh::VertexHandle& secondVH,
    const PolyMesh::VertexHandle& thirdVH)
{

    std::vector<std::pair<PolyMesh::VertexHandle, double>> vertexAngleList =
        getVertexAngleList(theMesh, currentVH, secondVH, thirdVH);

    double lastValue = vertexAngleList.back().second;

    if (lastValue < 40)
    {
        return PolyMesh::InvalidVertexHandle;
    }
    else if (lastValue <= 125)
    {
        if (!checkTriaByVertex(theMesh, currentVH,
            vertexAngleList.back().first,
            vertexAngleList[vertexAngleList.size() - 2].first))
        {
            return vertexAngleList[vertexAngleList.size() - 2].first;
        }
        else {
            // otherwise return the "third vertex"
            return vertexAngleList.back().first;
        }
    }
    else if (lastValue <= 200)
    {
        // Check for existing vertices
        double bisectorAngle = lastValue / 2.0;
        double threshAngle1 = bisectorAngle - 23.0;
        double threshAngle2 = bisectorAngle + 23.0;
        for (auto vh_angPair : vertexAngleList) {
            if (vh_angPair.second >= threshAngle1 && (lastValue - vh_angPair.second) >= threshAngle1) {
                return vh_angPair.first;
            }
        }
        
        // otherwise find the center tria to swap/split
        PolyMesh::VertexHandle preVertex;
        for (auto vh_angPair : vertexAngleList) {
            if (vh_angPair.second > threshAngle2) {
                return getSwapSplitTria(theMesh, currentVH, secondVH, thirdVH, preVertex, vh_angPair.first, threshAngle1);
            }
            preVertex = vh_angPair.first;
        }
        return PolyMesh::InvalidVertexHandle;
    }
    else {
        // find the
        int minAngle = 1000;
        PolyMesh::VertexHandle minVertex;
        for (auto vh_angPair : vertexAngleList) {
            double tempAngle = fabs(vh_angPair.second - 90.0);
            if (tempAngle < minAngle) {
                minAngle = tempAngle;
                minVertex = vh_angPair.first;
            }
        }
        return minVertex;
    }
}





PolyMesh::VertexHandle getSwapSplitTria(PolyMesh& theMesh,
    const PolyMesh::VertexHandle& currentVH,
    const PolyMesh::VertexHandle& secondVH,
    const PolyMesh::VertexHandle& thirdVH,
    const PolyMesh::VertexHandle& leftVH,
    const PolyMesh::VertexHandle& rightVH,
    double threshAngle1)
{

    PolyMesh::FaceHandle splitTriaHandle = getTriaByVertex(theMesh, currentVH, leftVH, rightVH);


    std::vector<PolyMesh::FaceHandle> leftVHtrias;
    for (PolyMesh::VertexFaceIter vf_it = theMesh.vf_iter(leftVH); vf_it.is_valid(); ++vf_it) {
        if (theMesh.valence(*vf_it) == 3) {
            leftVHtrias.push_back(*vf_it);
        }
    }
    std::vector<PolyMesh::FaceHandle> reflectTrias;
    for (PolyMesh::VertexFaceIter vf_it = theMesh.vf_iter(rightVH); vf_it.is_valid(); ++vf_it) {
        if (theMesh.valence(*vf_it) == 3 &&
            std::find(leftVHtrias.begin(), leftVHtrias.end(), *vf_it) != leftVHtrias.end())
        {
            reflectTrias.push_back(*vf_it);
        }
    }

    for (auto triaHandle : reflectTrias) {
        std::set<PolyMesh::VertexHandle> node_set;
        for (PolyMesh::FaceVertexIter fv_it = theMesh.fv_iter(splitTriaHandle); fv_it.is_valid(); ++fv_it) {
            node_set.insert(*fv_it);
        }
        for (PolyMesh::FaceVertexIter fv_it = theMesh.fv_iter(triaHandle); fv_it.is_valid(); ++fv_it) {
            node_set.insert(*fv_it);
        }
        node_set.insert(leftVH);
        node_set.insert(rightVH);
        if (node_set.size() == 4 &&
            std::find(node_set.begin(), node_set.end(), secondVH) == node_set.end() &&
            std::find(node_set.begin(), node_set.end(), thirdVH) == node_set.end()) {
            node_set.erase(leftVH);
            node_set.erase(rightVH);
            node_set.erase(currentVH);

            PolyMesh::VertexHandle reflectVH = *node_set.begin();

            double angle1 = getAngle(theMesh, reflectVH, currentVH, secondVH);
            double angle2 = getAngle(theMesh, reflectVH, currentVH, thirdVH);
            double length1 = getDistance(theMesh, reflectVH, currentVH);
            double length2 = (getDistance(theMesh, currentVH, secondVH) + getDistance(theMesh, currentVH, thirdVH))*0.75;
            if (angle1 >= threshAngle1 && angle2 >= threshAngle1 && length1 <= length2) {

                theMesh.request_vertex_status();
                theMesh.request_edge_status();
                theMesh.request_face_status();

                // swap
                theMesh.delete_face(splitTriaHandle, false);
                theMesh.delete_face(triaHandle, false);
                theMesh.garbage_collection();

                PolyMesh::FaceHandle newTria1 = theMesh.add_face(rightVH, reflectVH, currentVH);
                PolyMesh::FaceHandle newTria2 = theMesh.add_face(leftVH, reflectVH, currentVH);
                if (!newTria1.is_valid()) {
                    newTria1 = theMesh.add_face(rightVH, currentVH, reflectVH);
                }
                if (!newTria2.is_valid()) {
                    newTria2 = theMesh.add_face(leftVH, currentVH, reflectVH);
                }

                return reflectVH;
            }
            else {
                // split
                PolyMesh::Point mid_point = (theMesh.point(leftVH) + theMesh.point(rightVH)) * 0.5;
                PolyMesh::VertexHandle new_vertex = theMesh.add_vertex(mid_point);

                theMesh.request_vertex_status();
                theMesh.request_edge_status();
                theMesh.request_face_status();

                theMesh.delete_face(splitTriaHandle, false);
                theMesh.delete_face(triaHandle, false);
                theMesh.garbage_collection(false);

                PolyMesh::FaceHandle newTria1 = theMesh.add_face(rightVH, currentVH, new_vertex);
                PolyMesh::FaceHandle newTria2 = theMesh.add_face(rightVH, reflectVH, new_vertex);
                PolyMesh::FaceHandle newTria3 = theMesh.add_face(leftVH, currentVH, new_vertex);
                PolyMesh::FaceHandle newTria4 = theMesh.add_face(leftVH, reflectVH, new_vertex);
                if (!newTria1.is_valid()) {
                    newTria1 = theMesh.add_face(rightVH, new_vertex, currentVH);
                }
                if (!newTria2.is_valid()) {
                    newTria2 = theMesh.add_face(rightVH, new_vertex, reflectVH);
                }
                if (!newTria3.is_valid()) {
                    newTria3 = theMesh.add_face(leftVH, new_vertex, currentVH);
                }
                if (!newTria4.is_valid()) {
                    newTria4 = theMesh.add_face(leftVH, new_vertex, reflectVH);
                }

                return new_vertex;
            }
        }
    }
    return PolyMesh::InvalidVertexHandle;
}

 

[calciffer]

Below is the sixth post in this series. In the third post we discussed how to keep single connected domain, which is the key to reduce the number of triangular meshes. But what if the initial triangulation result is multiple connected domain? Look at the picture below



The image above is a very special example that I designed on purpose. There are two boundary edge loops in the picture, which means that the initial triangulation is a 2-connected domain. Assuming that the outer boundary edge loop is the current edge loop and the red line is the current edge, we will find that we cannot use vh1, vh2, vh2_align and vh1_align to generate the quadrilateral element because it violates the rules in the third post.

If we don't consider the rules in the third post for a moment, you can see that after using vh1, vh2, vh2_align, and vh1_align to generate the quadrilateral element, the entire model becomes single connected. This process can be used to reduce the number of boundary edge loops in the model.

Considering the rules in the third post and the process of reducing the number of boundary edge loops in the model above, I would like to propose the following rules

• For the current edge loop, the operation to reduce the number of boundary edge loops of the model can be performed only once
• vh1_align and vh2_align must satisfy the rules set in the fifth post
• vh1_align and vh2_align do not belong to the current edge loop
• vh1_align and vh2_align must be directly connected

The picture below indicates the situation of next edge in the current edge loop.

 

[calciffer]

This is the seventh in a series of posts on the full quadrilateral mesh generation method. Look at the picture below



When the Angle corresponding to the two vertices of edge is too large, following the algorithm in the first paper, a quadrilateral element with a longer opposite side edge will be generated, as shown in face1 in the figure. If you want to avoid generating quadrilateral elements with a longer opposite side edge, you need to properly encrypt the mesh at the rounded corners, as shown below, producing a washer-like effect. So another solution, as shown in face2 in the figure, is to directly look for nearby triangular faces to merge.

 

[calciffer]

Here is the first part of the 8th post in a series of posts on the full quadrilateral mesh generation method. Please look at the picture below.



I added two functions to solve the problem 2 mentioned in the first post. The principle is very simple, if you are familiar with openmesh library, you can easily understand the code below.

void localCloseAlignQuad(PolyMesh& theMesh,
    vtkSmartPointer<vtkPoints>&   thePoints,
    vtkSmartPointer<vtkPolyData>& thePolyData,
    vtkSmartPointer<vtkRenderWindow>& theRender)
{
    int closeFlag = 1;
    while (closeFlag) {
        closeFlag = 0;


        std::vector<PolyMesh::EdgeHandle> faceEdges;
        findFaceEdges(theMesh, faceEdges);

        std::set<PolyMesh::VertexHandle> boundaryVertices;
        getEdgeVertices(theMesh, faceEdges, boundaryVertices);

        for (PolyMesh::FaceIter f_it = theMesh.faces_begin(); f_it != theMesh.faces_end(); ++f_it) {
            PolyMesh::FaceHandle fh = *f_it;
            if (theMesh.valence(fh) == 4)
            {
                int bounaryFlag = 0;
                for (PolyMesh::FaceEdgeIter fe_it = theMesh.fe_iter(fh); fe_it.is_valid(); ++fe_it) {
                    PolyMesh::EdgeHandle eh = *fe_it;

                    PolyMesh::HalfedgeHandle heh1 = theMesh.halfedge_handle(eh, 0);
                    PolyMesh::HalfedgeHandle heh2 = theMesh.halfedge_handle(eh, 1);
                    PolyMesh::FaceHandle fh1 = theMesh.face_handle(heh1);
                    PolyMesh::FaceHandle fh2 = theMesh.face_handle(heh2);

                    if (!fh1.is_valid() || !fh2.is_valid()) {
                        bounaryFlag = 1;
                        break;
                    }
                }
                if (bounaryFlag == 1) {
                    continue;
                }
                std::vector< PolyMesh::VertexHandle > quadVertices;
                for (PolyMesh::FaceVertexIter fv_it = theMesh.fv_iter(fh); fv_it.is_valid(); ++fv_it) {
                    quadVertices.push_back(*fv_it);
                }
                if (theMesh.valence(quadVertices[0]) == 3 &&
                    theMesh.valence(quadVertices[2]) == 3 &&
                    std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[0]) == boundaryVertices.end() &&
                    std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[2]) == boundaryVertices.end())
                {
                    theMesh.request_vertex_status();
                    theMesh.request_edge_status();
                    theMesh.request_face_status();

                    theMesh.delete_face(fh, false);
                    theMesh.garbage_collection(false);

                    autoAddFace(theMesh, quadVertices[0], quadVertices[2], quadVertices[1]);
                    autoAddFace(theMesh, quadVertices[0], quadVertices[2], quadVertices[3]);

                    PolyMesh::HalfedgeHandle halfEdgeHandle = theMesh.find_halfedge(quadVertices[0], quadVertices[2]);
                    if (theMesh.is_valid_handle(halfEdgeHandle)) {
                        theMesh.collapse(halfEdgeHandle);
                        closeFlag = 1;
                        break;
                    }
                }
                else if (theMesh.valence(quadVertices[1]) == 3 && theMesh.valence(quadVertices[3]) == 3 && std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[1]) == boundaryVertices.end() && std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[3]) == boundaryVertices.end())
                {
                    theMesh.request_vertex_status();
                    theMesh.request_edge_status();
                    theMesh.request_face_status();

                    theMesh.delete_face(fh, false);
                    theMesh.garbage_collection(false);

                    autoAddFace(theMesh, quadVertices[1], quadVertices[3], quadVertices[0]);
                    autoAddFace(theMesh, quadVertices[1], quadVertices[3], quadVertices[2]);

                    PolyMesh::HalfedgeHandle halfEdgeHandle = theMesh.find_halfedge(quadVertices[1], quadVertices[3]);
                    if (theMesh.is_valid_handle(halfEdgeHandle)) {
                        theMesh.collapse(halfEdgeHandle);
                        closeFlag = 1;
                        break;
                    }
                }
            }
        }
    }
    updateVtkView(thePoints, thePolyData, theRender, theMesh);
}

 

[calciffer]

Here is the second part of the 8th post in a series of posts on the full quadrilateral mesh generation method. The second function is here.

void localAdjustIStyle(PolyMesh& theMesh,
    vtkSmartPointer<vtkPoints>&   thePoints,
    vtkSmartPointer<vtkPolyData>& thePolyData,
    vtkSmartPointer<vtkRenderWindow>& theRender)
{
    int adjustFlag = 1;
    while (adjustFlag) {
        adjustFlag = 0;

        std::vector<PolyMesh::EdgeHandle> faceEdges;
        findFaceEdges(theMesh, faceEdges);
        std::set<PolyMesh::VertexHandle> boundaryVertices;
        getEdgeVertices(theMesh, faceEdges, boundaryVertices);

        for (PolyMesh::FaceIter f_it = theMesh.faces_begin(); f_it != theMesh.faces_end(); ++f_it) {
            PolyMesh::FaceHandle fh = *f_it;
            if (theMesh.valence(fh) == 4)
            {
                int bounaryFlag = 0;
                for (PolyMesh::FaceEdgeIter fe_it = theMesh.fe_iter(fh); fe_it.is_valid(); ++fe_it) {
                    PolyMesh::EdgeHandle eh = *fe_it;

                    PolyMesh::HalfedgeHandle heh1 = theMesh.halfedge_handle(eh, 0);
                    PolyMesh::HalfedgeHandle heh2 = theMesh.halfedge_handle(eh, 1);
                    PolyMesh::FaceHandle fh1 = theMesh.face_handle(heh1);
                    PolyMesh::FaceHandle fh2 = theMesh.face_handle(heh2);

                    if (!fh1.is_valid() || !fh2.is_valid()) {
                        bounaryFlag = 1;
                        break;
                    }
                }

                if (bounaryFlag == 1) {
                    continue;
                }

                std::vector< PolyMesh::VertexHandle > quadVertices;

                for (PolyMesh::FaceVertexIter fv_it = theMesh.fv_iter(fh); fv_it.is_valid(); ++fv_it) {

                    quadVertices.push_back(*fv_it);

                }

                if (theMesh.valence(quadVertices[0]) == 3 && theMesh.valence(quadVertices[1]) == 3 && std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[0]) == boundaryVertices.end() && std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[1]) == boundaryVertices.end())

                {
                        localAdjustIStyle(theMesh, quadVertices[0], quadVertices[1]);
                  adjustFlag = 1;
                  break;
                }

                else if (theMesh.valence(quadVertices[1]) == 3 && theMesh.valence(quadVertices[2]) == 3 && std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[1]) == boundaryVertices.end() && std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[2]) == boundaryVertices.end())

                {
                  localAdjustIStyle(theMesh, quadVertices[1], quadVertices[2]);
                  adjustFlag = 1;
                  break;
                }

                else if (theMesh.valence(quadVertices[2]) == 3 && theMesh.valence(quadVertices[3]) == 3 && std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[2]) == boundaryVertices.end() && std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[3]) == boundaryVertices.end())

                {
                  localAdjustIStyle(theMesh, quadVertices[2], quadVertices[3]);
                  adjustFlag = 1;
                  break;
                }

                else if (theMesh.valence(quadVertices[0]) == 3 && theMesh.valence(quadVertices[3]) == 3 && std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[0]) == boundaryVertices.end() && std::find(boundaryVertices.begin(), boundaryVertices.end(), quadVertices[3]) == boundaryVertices.end())

                {
                  localAdjustIStyle(theMesh, quadVertices[0], quadVertices[3]);
                  adjustFlag = 1;
                  break;
                }
            }
        }
        combineQuadWithInteriorVertex(theMesh);
    }

    updateVtkView(thePoints, thePolyData, theRender, theMesh);

}




void localAdjustIStyle((PolyMesh& theMesh,
    PolyMesh::VertexHandle vh1,
    PolyMesh::VertexHandle vh2)
{
    PolyMesh::HalfedgeHandle heh = theMesh.find_halfedge(vh1, vh2);
   PolyMesh::EdgeHandle eh = theMesh.edge_handle(heh);

   // 获取与边缘相邻的两个面
   PolyMesh::HalfedgeHandle heh1 = theMesh.halfedge_handle(eh, 0);
   PolyMesh::HalfedgeHandle heh2 = theMesh.halfedge_handle(eh, 1);
   PolyMesh::FaceHandle fh1 = theMesh.face_handle(heh1);
   PolyMesh::FaceHandle fh2 = theMesh.face_handle(heh2);

   unsigned int fh_val = 100;
   PolyMesh::FaceHandle fh_new;
   PolyMesh::VertexHandle vh_new;
   std::vector< PolyMesh::FaceHandle > fhs_new = { fh1 , fh2 };
   std::vector< PolyMesh::VertexHandle > vhs_new = {vh1, vh2};

   for (auto tempfh : fhs_new) {
       for (auto tempvh : vhs_new) {
           if (theMesh.valence(sortQuadVertices(theMesh, tempfh, tempvh)[3]) < fh_val) {
               fh_val = theMesh.valence(sortQuadVertices(theMesh, tempfh, tempvh)[3]);
               fh_new = tempfh;
               vh_new = tempvh;
           }
       }
   }



   std::vector< PolyMesh::VertexHandle > quadVerticesNew = sortQuadVertices(theMesh, fh_new, vh_new);
   theMesh.request_vertex_status();
   theMesh.request_edge_status();
   theMesh.request_face_status();
   theMesh.delete_face(fh_new, false);
   theMesh.garbage_collection(false);

   autoAddFace(theMesh, quadVerticesNew[0], quadVerticesNew[3], quadVerticesNew[1]);
   autoAddFace(theMesh, quadVerticesNew[0], quadVerticesNew[3], quadVerticesNew[2]);

   PolyMesh::HalfedgeHandle halfEdgeHandle = theMesh.find_halfedge(quadVerticesNew[0], quadVerticesNew[3]);

   if (theMesh.is_valid_handle(halfEdgeHandle)) {
       theMesh.collapse(halfEdgeHandle);
   }
}

 

[calciffer]

This is the ninth post and the second to last post on full quadrilateral mesh generation algorithms. I would like to discuss the issues left open in the third post.
The picture below is also taken from the paper

汪攀,张见明,韩磊等.基于带约束前沿推进的四边形网格生成方法.湖南大学学报(自然科学版),2017,44(08):29-34.

As you can see, for the front edge AB, if CE forms the top edge, the four points A,B,C,E fail to generate a quad element because it violates the rule we proposed in the third post.

If the return value of the function equal to -1, we split the triangle ACE into three triangles, then four points A,B,C, and F can generate a quad element. There is a function called split in openmesh library that can be used.

In general, I'm not against using two triangles to form a quadrilateral, as long as we can guarantee that connected regions are simply connected or, more accurately, that the number of connected regions does not increase. Although it is diffcult to control the mesh flow direction when two triangles are directly merged into a quadrilateral, there are many ways to smooth and optimize the mesh after generating the full quadrilateral mesh, and the influence of grid flow direction on the accuracy of structural analysis is not unacceptable.

 

[calciffer]

This post is the last one on the full quadrilateral mesh generation method. Today we will discuss the case where the model has multiple surfaces.
In the actual mesh generation process, we rarely encounter a situation where we only need to mesh independent faces, and the faces we encounter are mostly connected to each other, just like the picture below.


In netgen, we can input the whole model directly, and then use netgen's GetSurfaceElementsOfFace function to get the triangulation of each face and store it in the polymesh data structure of openmesh library.
Netgen's triangulation algorithm is very efficiency. As you can see in the picture below, it took only 0.16 seconds to generate 3366 triangles, including the time it took to write to the openmesh library.



And the code is here

for (int fidx = 1; fidx <= occgeo.fmap.Extent(); ++fidx)
    {
        PolyMesh faceMesh;

        for (int i = 1; i <= nbNodes; ++i)
        {
            const netgen::MeshPoint& point = ngMesh.Point(netgen::PointIndex(i));
            PolyMesh::VertexHandle vh = faceMesh.add_vertex(PolyMesh::Point(point[0], point[1], point[2]));
        }

        netgen::Array<netgen::SurfaceElementIndex> elemIds;
        ngMesh.GetSurfaceElementsOfFace(fidx, elemIds);


        for (const auto& elemId : elemIds)
        {
            const netgen::Element2d& elem = ngMesh.SurfaceElement(netgen::ElementIndex(elemId+1));
            if (elem.GetNP() == 3)
            {
                PolyMesh::FaceHandle fh = faceMesh.add_face(
                    PolyMesh::VertexHandle(elem[0] - 1),
                    PolyMesh::VertexHandle(elem[1] - 1),
                    PolyMesh::VertexHandle(elem[2] - 1));
            }

            if (elem.GetNP() == 4)
            {
                PolyMesh::FaceHandle fh = faceMesh.add_face(
                    PolyMesh::VertexHandle(elem[0] - 1),
                    PolyMesh::VertexHandle(elem[1] - 1),
                    PolyMesh::VertexHandle(elem[2] - 1),
                    PolyMesh::VertexHandle(elem[3] - 1));
            }
        }

        faceMesh.garbage_collection();
        theMeshes.push_back(faceMesh);
    }

The triangulation of each surface is then transformed into a full quadrilateral mesh by the previous algorithm, and finally all faces are merged.

As you can see in the figure below, without updating the view, the algorithm takes 0.48 seconds to convert 3366 triangular elements into 1551 quadrilateral elements and 4 triangular elements, which is reasonably efficient.
To be honest, I'm not worried about efficiency, my experience with c++ is very limited, and there must be space for improvement for this method, both in time and space complexity.

 

[synt]

hi,

to set edge division of circle, it can be use parameter file of 'maxh' in Netgen. An example of circle with 10 unit diameter needed to have 12 divisions, so the value 'maxh' is 2.618 unit

in case of many circle with combined objects, another developer creates mesh refinement file based on 32 point of circle coordinates and set to the values as before.

p. s : i'm not a programmer, only known work around about the mesher interact but not deeply in codes.

 

[calciffer]

hi,

to set edge division of circle, it can be use parameter file of 'maxh' in Netgen. An example of circle with 10 unit diameter needed to have 12 divisions, so the value 'maxh' is 2.618 unit

in case of many circle with combined objects, another developer creates mesh refinement file based on 32 point of circle coordinates and set to the values as before.

p. s : i'm not a programmer, only known work around about the mesher interact but not deeply in codes.

Hi, synt

As far as I know, netgen does not strictly obey maxh and minh parameters when doing triangulation, and I am not sure whether a triangulation with an even number of boundary nodes can be obtained by setting the maxh parameter.

But there are other ways to set the number of nodes directly in the netgen library, see the link below

https://forum.ngsolve.org/t/how-to-control-the-number-of-boundary-nodes-in-netgen/2398

To be honest, I think it is acceptable for at most one triangle element of each face .

 

[calciffer]

That all looks amazingly interesting, although it would require a deep dive into quadmesh generation field to constructively comment on your achievements. I'll pin the topic to be always on top for now, so other folks can find it more easily.

Hi, Quaoar

Thank you very much, I hope these posts can help anyone who is interested in this topic.

 

[synt]

As far as I know, netgen does not strictly obey maxh and minh parameters when doing triangulation,

it seems to be right, previously i'm testing on tetrahedral volume mesh. Each edge need to be defined in mesh refinement files to achieved desire results.

maxh = 100
minh = 0
grading =0.1

 

[calciffer]

Each edge need to be defined in mesh refinement files to achieved desire results.

Hi, synt

I am not sure what do you mean by "Each edge need to be defined in mesh refinement files".
Is there any way to control the number of nodes on the edge via mesh refinement files?
I'm not familiar with the netgen library, and there aren't many usage examples.

 

[synt]

Is there any way to control the number of nodes on the edge via mesh refinement files?

Hi Calciffer

yes, it's possible to control local mesh to do refinement and NetGen took the lower values of global and local parameter (e.g figure below). It seems, i need to look in the codes after your great contribution is completely implemented in Analysis Situs.

Regards,