Rebuild edge

Topological condition

To rebuild an edge by re-intersecting its neighbor faces, use rebuild-edge command. Analysis Situs will analyze the local topological condition around the edge trying to find the support faces to intersect (faces s1 and s2 in the following figure).

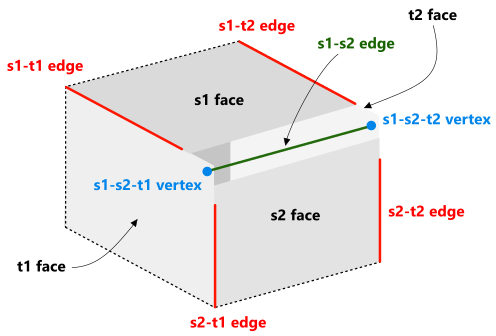
As the figure above shows, in the simplest situation, we have ten adjacent topological elements for the edge in question (denoted as s1-s2). This tuple of ten boundary elements we call a topological condition which requires a certain geometric resolution. It is assumed that resolution does not change the topology of the model. If any topological changes are required, consider applying Euler operators.

Faces s1 and s2 are chosen w.r.t. the orientation of the target edge. The face which contains a coedge oriented equally with s1-s2 edge is chosen as s1 without reducing the generality. The vertex s1-s2-t1 is chosen as the first vertex of the edge s1-s2. The vertex s1-s2-t2 is chosen as the last vertex of the edge s1-s2.

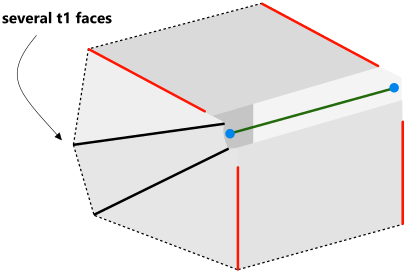
There can be more than just a couple of terminating faces t1 and t2 as the figure above shows. If so, there will be a fan of s*-t* edges which should not be forgotten. At the same time, the s-t edges are not required for the geometric computations themselves, and it is only necessary to take them into account when constructing a modification history (e.g., to preserve metadata).

Knowledge-guided computation

The process of edge rebuilding employs recomputation of its host curve and extremities (i.e. vertices). However, in some circumstances you may know a priori that no recomputation is necessary for certain vertex positions. This knowledge can be taken into account in the algorithm by specifying the so called "frozen" vertices. Let's expand a bit on why this possibility is important. A vertex is generally recomputed using curve-surface intersection algorithm. However, if the intersection operands are not in general position (see [Barnhill et al, 1987] for the discussion of "general position" term in the context of intersection), the recomputation routine is likely to fail or give inaccurate results. The figure below illustrates two situations which are tricky to resolve. In the fist figure, the intersection point was not found because of small proximity between the operands. Such a proximity has no sense from the engineering point of view as most likely the geometries are meant to be tangent. The next figure illustrates a possible result of intersection if the operand curve is pulled a bit closer to the surface. We see multiple intersection points (none is accurate) while only one point is actually meant there.

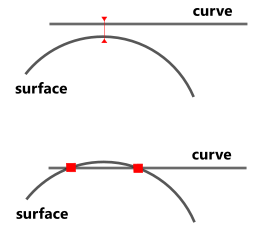
The best practice in geometric modeling is to identify special cases of intersection to enable specific treatment for them. Since multiple intersection points may emerge in tangential cases, the rebuild-edge command attempts to average the obtained points to produce a single result out of them. However, this technique is error-prone as it does not guarantee that the average point is more accurate than any of the contributing positions. In practice, it is much better just to avoid recomputation of intersections as much as possible (and especially in non-general-position cases). The possibility to specify the "frozen" vertices enables the principle known as "knowledge-guided computation" (see [Piegl, 2005] for a comprehensive discussion of robustness issues in CAD).

One practical example where "frozen" vertices are used is a blends suppression algorithm. In this algorithm, the edge s1-s2 is the image of the collapsed blend face, and the edges s1-t1, s2-t1, s1-t2 and s2-t2 require recomputation. Each of the latter edges has one vertex which does not require recomputation (the vertex on the back face which is not touched by the operation).

The following animation shows an example where the recognition of frozen vertices allowed us to escape from a numerical instability and remove faces which could not be suppressed by a general-purpose removal operator.