NURBS modeling

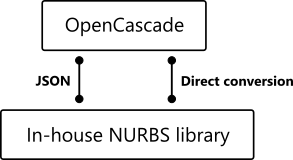
Analysis Situs uses two geometric modeling kernels. The main kernel is OpenCascade. Another one is the in-house NURBS modeling kernel developed following the classic monography by L. Piegl and W. Tiller, The NURBS Book. In this chapter, we present the basic NURBS modeling functionality available in Analysis Situs without emphasizing the difference between the two kernels.

Basic algorithms

Point inversion for surface

The point inversion algorithm for B-surface is based on Newton iterations following the approach presented in The NURBS Book. The input for this calculation is the coordinates of a 3D point. The output is the parametric (u,v) image which gives a point projected on a surface. Use invert-point-surf Tcl command for point-surface inversion.

Decompose B-curve into Bezier segments

Bezier decomposition is one of the fundamental algorithms for manipulating NURBS-based geometry. It is known that any B-curve can be represented as a tuple of Bezier curves without distortion. The curve splitting technique implemented in Analysis Situs follows the algorithm A5.6 from The NURBS Book. Use split-curve-bezier Tcl command to decompose a B-curve into the equivalent collection of Bezier curves.

Flip parameterization

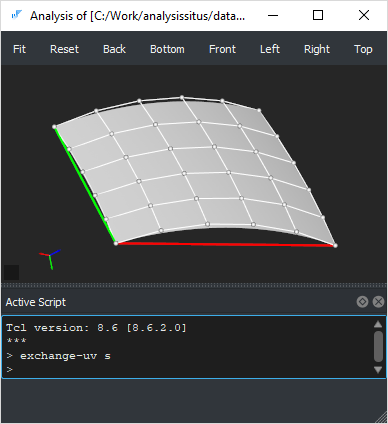
To exchange curvilinear U and V axes of a B-surface, use exchange-uv Tcl command. The curvilinear axes are visualized with small red (U axis) and green (V axis) glyphs starting at the first pole. Exchanging U and V parameters does not change the surface shape but flips the axes.

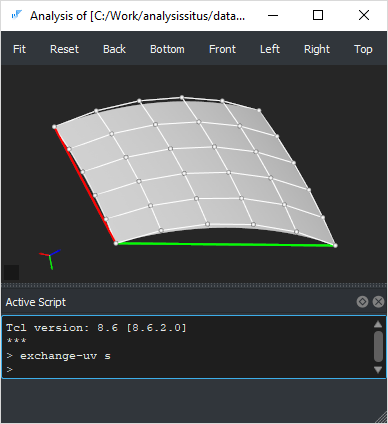
After flipping:

Curve knot insertion

Knot insertion into a B-spline curve is implemented following the algorithm A5.1 from The NURBS Book. To perform knot insertion, use insert-knot-curve Tcl command.

Surface knot insertion

Knot insertion into a B-spline surface is implemented following the algorithm A5.3 from The NURBS Book. To perform knot insertion, use insert-knot-surf-u and insert-knot-surf-v Tcl commands.

Modeling operators

Surface fairing

You can find the details on surface fairing in the dedicated page.

Services

Create primitive from JSON

You can create a B-curve or a B-surface from its JSON representation using define-geom Tcl command. In the opened dialog, you will have to type the name of the geometric entity and its textual representation.

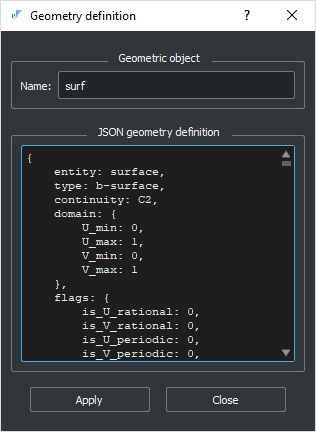
Here is an example of a valid B-surface JSON representation (try copying and pasting it to the dialog opened with define-geom command):

{
  entity: surface,
  type: b-surface,
  continuity: C0,
  domain: {
    U_min: 0,
    U_max: 1,
    V_min: 0,
    V_max: 1
  },
  flags: {
    is_U_rational: 0,
    is_V_rational: 0,
    is_U_periodic: 0,
    is_V_periodic: 0,
    is_U_closed: 0,
    is_V_closed: 0
  },
  properties: {
    U_degree: 1,
    V_degree: 1,
    U_knots: [0, 0, 0.5, 1, 1],
    V_knots: [0, 0, 0.5, 1, 1],
    num_poles_in_U_axis: 3,
    num_poles_in_V_axis: 3,
    poles: {
      u0: [[-10, -10, 0], [-10, 0, 0], [-10, 10, 0]],
      u1: [[0, -10, 0], [0, 0, 10], [0, 10, 0]],
      u2: [[10, -10, 0], [10, 0, 0], [10, 10, 0]]
    }
  }
}

In case you start from an existing CAD model, you can obtain a JSON dump by selecting the B-surface of interest and using the context menu as shown in the following animation: